2D Rotation Matrix Derivation
We start with a vector $\mathbf{v}$ on the Cartesian plan at coordinates $(x, y)$ which we rotate by an angle $\theta$ to our transformed point $\mathbf{v’}$ at $(x’, y’)$.
We want our $2\times 2$ rotation matrix to be a function of theta such that \(\begin{bmatrix}a & b \\ c & d\end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}x' \\ y'\end{bmatrix}\)
Or equivalently,
\[\mathbf{R(\theta)v} = \mathbf{v'}\]How can we go about solving for $a, b, c, d$?
We can introduce another angle $\phi$ as the angle between the $x$-axis and $\mathbf{v}$ and represent $\mathbf{v}$ in polar coordinates. This is because polar coordinates already use angular rotations, so when we want to get $\mathbf{v’}$, we keep $\mathbf{v}$'s magnitude $r$ and just add $\theta$ to the angle of our polar vector.
Here is a picture of our current setup:
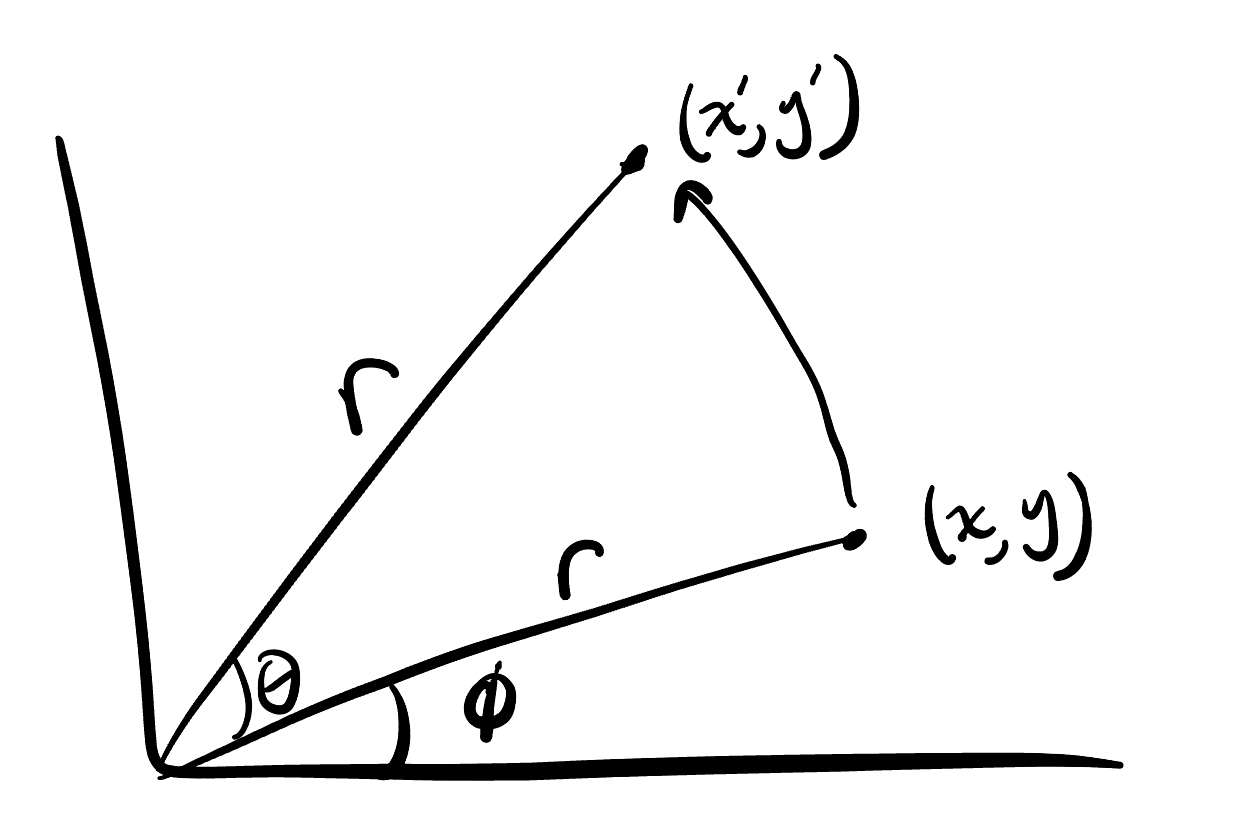
With
\(\mathbf{v} = (r \cos(\phi), r \sin(\phi))\) \(\mathbf{v'} = (r \cos(\phi+\theta), r \sin(\phi+\theta))\)
Then
\[\begin{bmatrix}a & b \\ c & d\end{bmatrix} \begin{bmatrix}r \cos(\phi) \\ r \sin(\phi)\end{bmatrix} = \begin{bmatrix}r \cos(\phi+\theta) \\ r \sin(\phi+\theta)\end{bmatrix}\]And multiplying out we get
\[ar\cos(\phi) + b r \sin(\phi) = r \cos(\phi+\theta)\] \[c r\cos(\phi) + d r \sin(\phi) = r \sin(\phi+\theta)\]Now using the angle addition identity, we can expand the RHS to get
\[ar\cos(\phi) + b r \sin(\phi) = r (\cos(\theta)\cos(\phi) - \sin(\theta)\sin(\phi))\] \[c r\cos(\phi) + d r \sin(\phi) = r (\sin(\theta)\cos(\phi) + \cos(\theta)\sin(\phi))\]Factoring out the $r$'s,
\[a\cos(\phi) + b \sin(\phi) = \cos(\theta)\cos(\phi) - \sin(\theta)\sin(\phi)\] \[c \cos(\phi) + d \sin(\phi) = \sin(\theta)\cos(\phi) + \cos(\theta)\sin(\phi)\]And by simple examination we can now see
\[a=\cos(\theta)\] \[b=-\sin(\theta)\] \[c=\sin(\theta)\] \[d=\cos(\theta)\]Therefore,
\[\mathbf{R(\theta)} = \begin{bmatrix}\cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta)\end{bmatrix}\]We now have a matrix to rotate any 2D vector by an angle $\theta$! Getting this matrix is very simple and straightforward, the key insight is to switch to polar form with an initial angle $\phi$, and then apply the angle addition identity that of course nobody remembers on the spot.
\[\square\]