Special Relativity Derivations
These are derivations of the three fundamental effects of special relativity, namely time dilation, length contraction, and rear-clock ahead effect. Special relativity was famously theorized by Albert Einstein in two of his four seminal papers of 1905. Special relativity deals with motion at relativistic speeds, near the speed of light ($c\approx 3\times 10^8$ m/s). It’s notoriously trippy to think about, because concepts like temporal and spacial simultaneity (things happening at the same time or position in space) become relative – one person might see things happening at the same time, while another might not, isn’t that crazy?
Special relativity comes from the fact that nothing in the universe can travel faster than the speed of light. Galilean (classical) relativity can result in adding velocities, which can result in contradictions of the above statement. For example, imagine you are in a car moving at $5$ m/s and throw a ball at $6$ m/s relative to you. From a standstill observer, the ball will be moving at $5+6=11$ m/s, this is how relative motion works in our everyday lives. No contradiction so far.
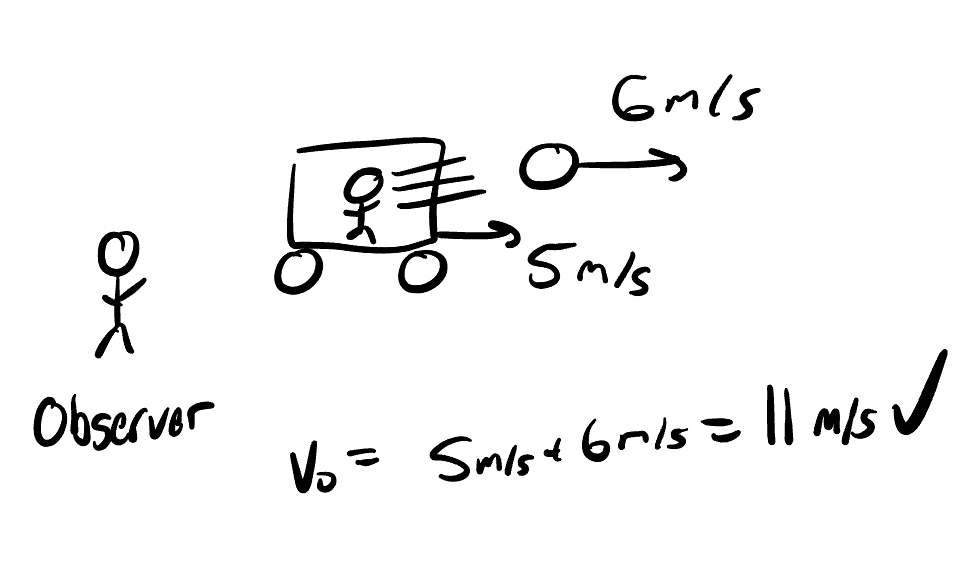
Now imagine the same scenario, but you are moving at $0.5c$ and you throw the ball at $0.6c$. Galilean relativity says a standstill observer should see the ball moving at $0.5c + 0.6c = 1.1c$, but this is greater than the speed of light. Contradiction! How can we resolve this? Well if you’re Einstein it’s by creating an entire new branch of theoretical physics:
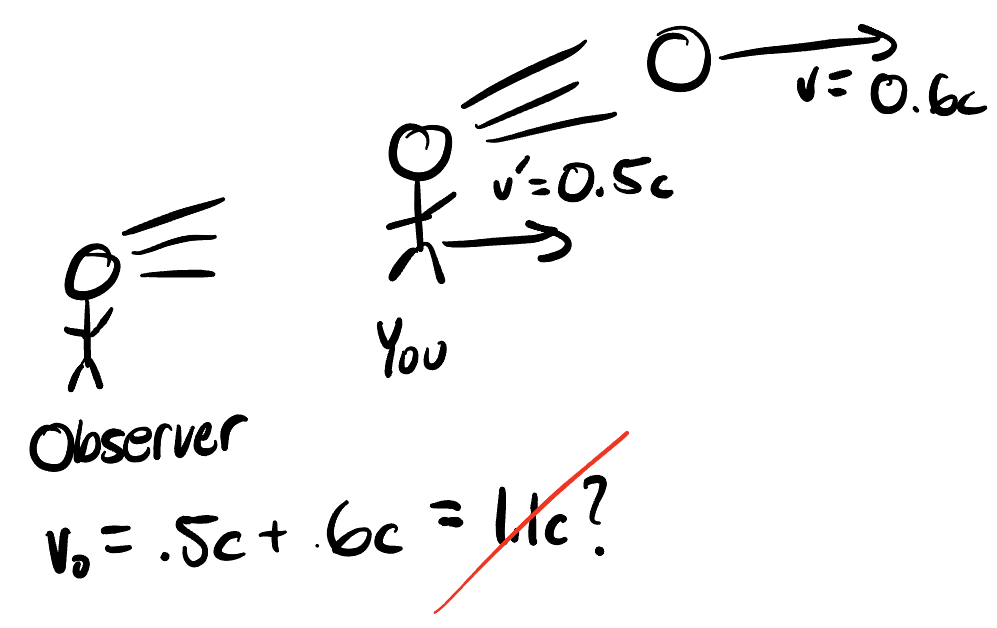
Effect 1: Time Dilation
Light always travels at the speed of light (who would have thought!), which results in time being relative as we’ll see very soon. Time dilation quantifies how we can relate times viewed by different observers based on their velocities relative to each other.
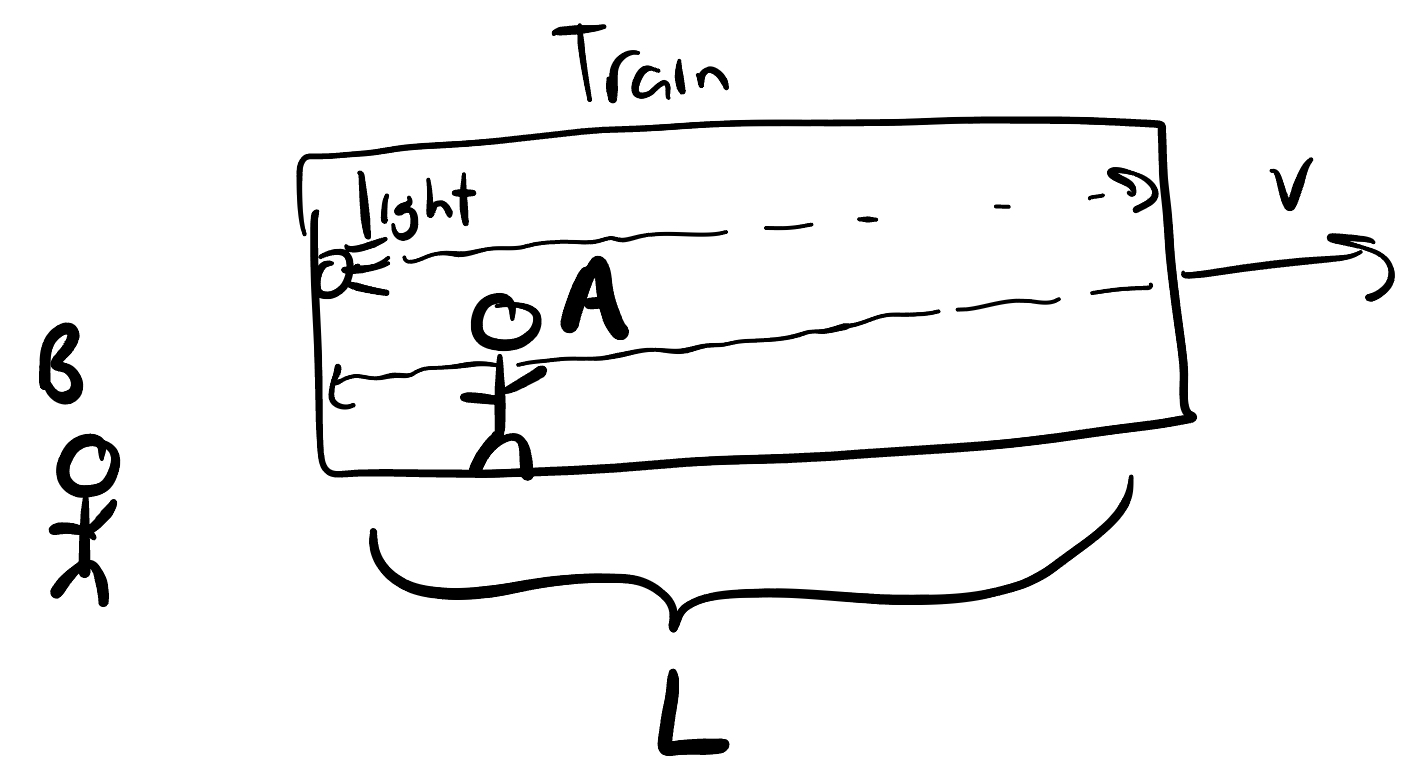
Let’s imagine a scenario where person A is on a train moving at velocity $v$, and person B is a stationary outside observer. Now also imagine there is a vertical laser pointer on the train that shoots light up to the ceiling of height $h$, where it bounces off a mirror and comes back down to its origin point. We are trying to determine how long A and B measure this sequence of events lasting.
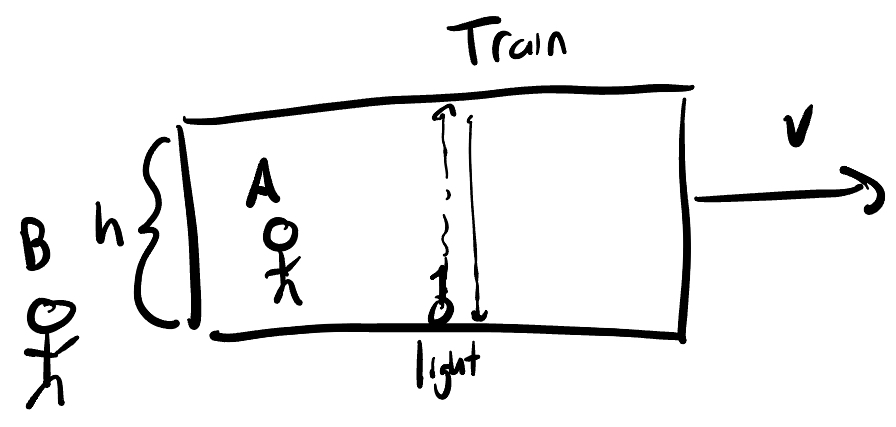
From A’s frame, this is pretty simple to calculate. The light moves at $c$, and travels a distance of $h$ up and $h$ down, so trusty $d=rt$ gives us a total time of $t_A = \frac{2h}{c}$
Things get a bit more tricky with B, since now the light’s velocity has a horizontal component of $v$ since it’s on the train. However, since the magnitude of the velocity of the light must be $c$, this means the vertical component, which we’ll call $y$ (the part we care about) is no longer $c$.
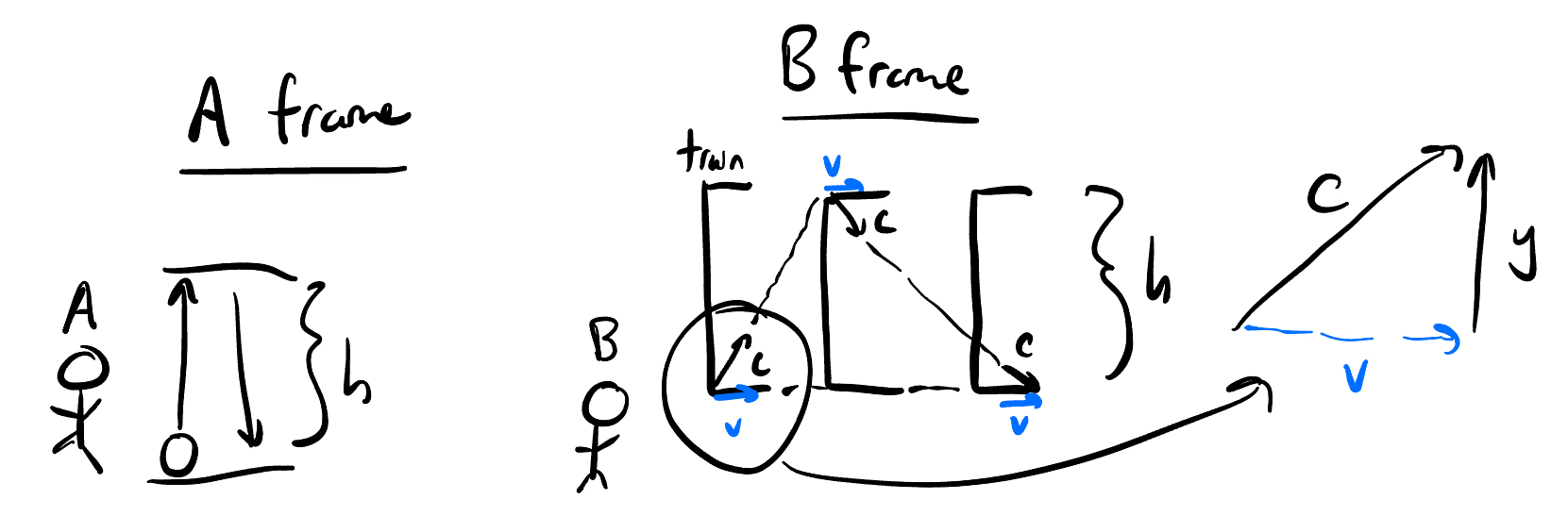
Using Pythagorean theorem and solving for $y$, we get
\[c^2 = v^2 + y^2\] \[y^2 = c^2-v^2\] \[y = \sqrt{c^2-v^2}\] \[D=rt \implies t_B = \frac{2h}{\sqrt{c^2-v^2}}\]Taking the ratio between $t_B$ and $t_A$, we get
\[\frac{\frac{\cancel{2h}}{\sqrt{c^2-v^2}}}{\frac{\cancel{2h}}{c}} = \frac{c}{\sqrt{c^2-v^2}} \cdot \frac{1/c}{1/c} = \frac{1}{\frac{\sqrt{c^2-v^2}}{c}} = \frac{1}{\sqrt{\frac{c^2-v^2}{c^2}}}\] \[\implies \frac{t_B}{t_A} = \frac{1}{\sqrt{1-v^2/c^2}} \equiv \gamma\]This means that the time elapsed differs between observers by this multiplicative factor we define as gamma. Gamma is a very important factor that comes up a lot in special relativity, which is why it has its own name. Notice that it’s dependent on $v$, and is always above 1 if you graph it.
Now if we define the proper reference frame as the frame in which the position does not change between the start and end of the event you are timing, then A is the proper observer, since in its frame, the laser pointer never moves. The proper observer measures proper time, while all other observers measure an improper time. This then gives us
\(\frac{t_{improper}}{t_{proper}} = \gamma\)
\[\boxed{t_{observed} = \gamma \cdot t_{proper}}\]This is time dilation! The gamma factor is dependent on $v$, so this applies for any reference frame moving at any velocity. The dilation part comes from the fact that since gamma is always above 1, the proper time is the smallest possible timing of an event. All other frames outside of the proper frame experience a larger amount of time elapsing, almost like the time “dilates” for them. Isn’t this crazy! For B, time moves slower, compared to A, and this actually happens in our universe. Astronauts have gone to space, come back after moving at large speeds compared to us for extended periods of time, and had their watches not synced up with ours anymore. Even the idea that you can sync up two watches, move them around, and compare them again and they won’t be synced up is insane. Time dilation is the reason we even see certain particles. Muons have a short decay lifetime, but because they move at relativistic speeds, we observe their decay lifetime dilated to something way larger, which allows them to reach us on Earth. In our reference frame, they exist, in their reference frame, they’ve already decayed! It’s really trippy to think about.
Effect 2: Length Contraction
Next up is length contraction. You always here about “spacetime” in relativity, so it makes sense that since time dilates, space has to do something to. As we’ll now see, it contractions! We use a similar scenario as before to exploit the constant velocity of light into quantifying how distances change between observers. Imagine B is an observer and A is still on the train of length $L$ moving at velocity $v$, but now the laser shoots light from the left end of the train to the right end, where it bounces off a mirror and returns back to its origin. We’ll once again be measuring the time this event takes for both A and B, but this time using $L_A$ for the length of the train in A’s frame, and $L_B$ for the length in B’s frame.
This is once again simple in A’s frame, since nothing is moving! The light travels $L_A$ there and $L_A$ back, giving $t_A = \frac{2L_A}{c}$
In B’s frame, the light travels the initial length of the train $L_B$, plus the distance the right end of the train moves during this time the light is also traveling to the right, so $vt$. This gives us a total distance traveled of $L_B+vt$ at the speed of light, so $t = \frac{L_B+vt}{c}$. Solving for $t$, we get
\[ct = L_B + vt \implies ct - vt = L_B \implies t(c-v) = L_B \implies t_{right} = \frac{L_B}{c-v}\]This handles the light hitting the right end of the train, now let’s consider the light returning back. Normally the light would have to travel $L_B$, but the left end of the train is moving towards you this entire time, so now we get $t = \frac{L_B-vt}{c}$. This is similar to the above expression, and solving gives
\[t_{left} = \frac{L_b}{c+v}\]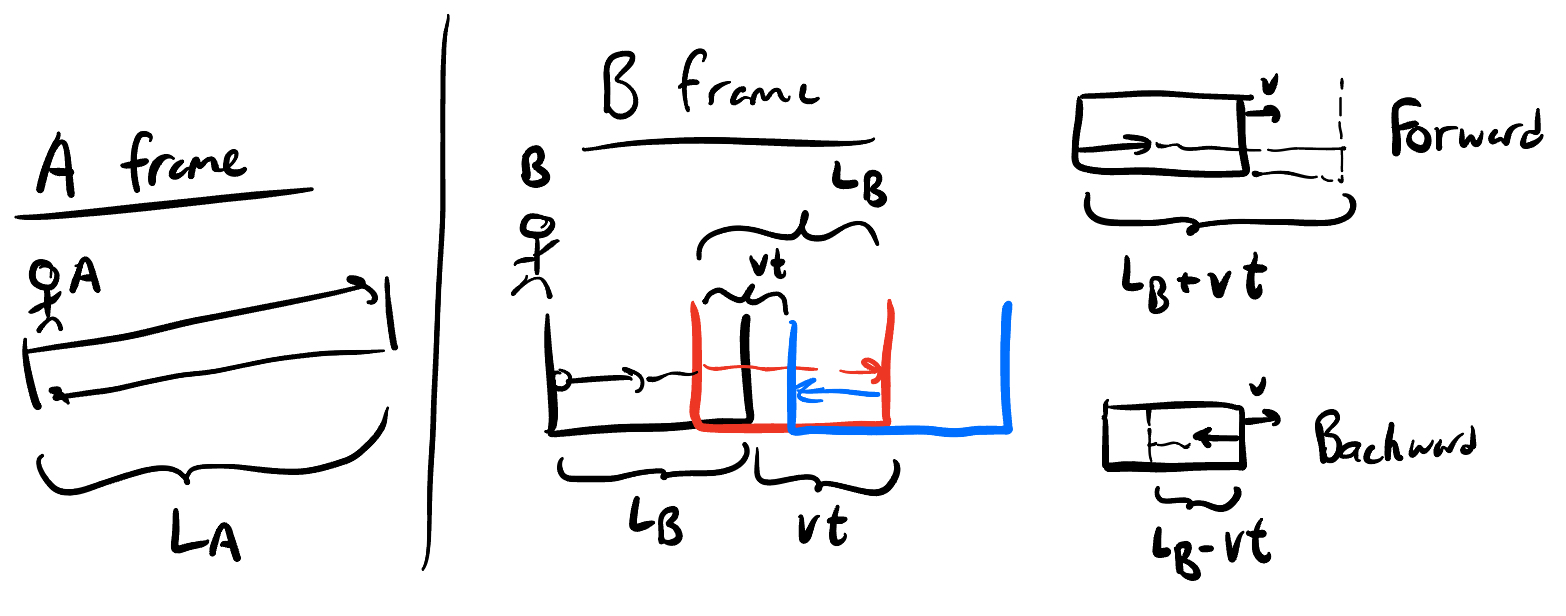
The total time is the time going right and left, so we have:
\[t_B = \frac{L_B}{c-v} + \frac{L_B}{c+v}\] \[= \frac{L_B(c+v)}{c^2-v^2} + \frac{L_B(c-v)}{c^2-v^2}\] \[= \frac{L_B c + \cancel{L_B v} + L_B c - \cancel{L_B v}}{c^2-v^2}\] \[= \frac{2 L_B c}{c^2-v^2} \cdot \frac{1/c^2}{1/c^2} = \frac{\frac{2L_B}{c}}{1-\frac{v^2}{c^2}}\] \[\implies t_B = \gamma^2 \frac{2L_B}{c}\]Now we can apply time dilation to relate our proper time (measured in A’s frame) to the improper time measured by B:
\[t_B = \gamma t_A\]So plugging in for $t_B$, and then plugging in for $t_A$, we get:
\[\gamma t_A = \gamma^2 \frac{2L_B}{c}\] \[\cancel{\gamma} \frac{\cancel{2}L_A}{\cancel{c}} = \gamma^{\cancel{2}} \frac{\cancel{2}L_B}{\cancel{c}}\] \[L_A = \gamma L_B\]Now we can define proper length as the length measured in the reference frame where the object you are measuring is not moving. In this case, this would be the length measured by A. So,
\[L_{proper} = \gamma \cdot L_{improper}\] \[\boxed{L_{observed} = \frac{L_{proper}}{\gamma}}\]This is length contraction! Notice that the contraction part comes from the fact that when you are in any reference frame other than the proper reference frame of a length, $v$ is nonzero, so $\gamma \ge 1$, so the length you observe is contracted (ie smaller) than the proper length. This is also a crazy idea, that a ruler can be different sizes to different people based on their reference frame!? You can also see how length contraction goes hand-in-hand with time dilation, we even use one for the other’s derivation! In all relativistic scenarios, both occur together, they’re inherently the same phenomenon, warping the bundled quantity that is spacetime.
Effect 3: Rear-Clock Ahead
Coming Soon
$\require{cancel} \cancel{2h}$